Interested in the compound interest spreadsheet used in the video? Click here.
Does compound interest apply to stocks? Video summary
Compounding helps investments grow at an ever-increasing rate.
Both assets and liabilities can compound. It can work for or against you.
The more frequent the compounding, the greater the return. All other things being equal.
What is compounding?
Capital gains, interest, or dividends that are reinvested to earn a higher return over time.
Earnings are generated from the initial investment and earnings are generated from previous periods’ earning. You earn “interest on interest.” The more earnings that have been compounded, the more earnings you are going to make every period. The “snowball” gets bigger and bigger.
Returns on the initial investment magnify over time. At some point, earning on earnings can eclipse earnings on the initial investment.
What is the power of compounding?
Compounding is related to the “time value of money.” The time value of money states that a dollar today is worth more than a dollar tomorrow.
Why? Because you could invest that dollar today and earn a return. Without it, you have an opportunity cost.
Compounding affects both assets and liabilities.
How so with liabilities?
Interest accumulates on unpaid principal, e.g. credit card. As you accrue interest on interest the amount you owe can grow faster than you can reduce principal.
What is the formula for calculating compound interest?
Future value = present value × (1 + interest rate) ^ number of periods
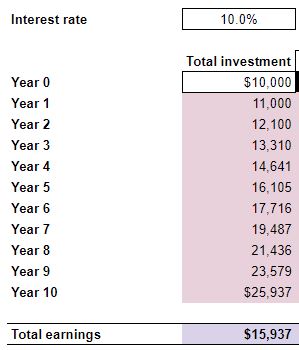
Using the example from the spreadsheet:
Future value = $10,000 × (1 + 10.0%) ^10
Future value = $10,000 × 2.5937
Future value = $25,937
$25,937 matches the Year 10 Total investment from the example spreadsheet.
Changing the variables for the compounding formula
▲ number of periods = ▲ future value
E.g. $10,000 × (1 + 10.0%) ^ 15 = $41,772
▲ interest rate = ▲ future value
E.g. $10,000 × (1 + 15.0%) ^ 10 = $40,456
▲ present value = ▲ future value
E.g. $15,000 × (1 + 10.0%) ^ 10 = $ 38,906
What if there are more than 1 compounding periods in a year?
As the frequency of compounding increases the future value increases. Even at the same rate of return.
12 compounding periods > 4 compounding periods > 1 compounding period
For example:
Present value = $10,000, interest rate = 10.0%, periods = 1
Compounded yearly, the future value is = $11,000
Compounded quarterly, the future value is = $11,038
Compounded monthly, the future value is = $11,047
Questions
“How do stocks earn compound interest?”
(Common) stocks don’t earn interest. They earn capital gains and dividends.
Capital gains compound if the stock keeps increasing in price every year.
Dividends compound if they are reinvested.
“How does compound interest work when investing in stocks?”
As earnings increase, the stock price will (generally) increase. This is because the company is worth more because it is (and is expected to continue) earning more money.
Also, dividends that are reinvested to buy more shares will, subsequently, earn more in dividends in the future.
“What is compounding in stocks?”
When returns from this year earn more returns next year.
This year’s and next year’s returns then earn more returns the year after that.
And so on…